It is expected that the information presented here will enable the reader to gain the basic concepts of computer programming. These concepts apply to common procedural language programming of a binary computer, yet they are language and computer independent. In this section the reader will learn how data (numbers and characters) are stored in a computer. In the next section, Programming Basics: Constructs, the reader will learn the basic programming constructs that instruct a computer to operate on data.

The American English language uses decimal numbers for the normal, default and natural expression of numbers. The decimal number system is taught to us from a very early age and we are now quite familiar with it. We do not usually even think about what components comprise the decimal number system. Yet, there are several concepts and terms that we have learned in order to use this system. The decimal number system is based on the powers of ten for the numbers place value and the digits 0 to 9. We call the system of basing the decimal number on the powers of ten a base 10 numbering system. This means that every place position for a digit is a greater power of ten as we increase a number from 0 to 10 to 100 and etc… The only digits we have are 0 to 9 for each place position in a number. For the one’s place we can have to numbers 0 to 9, represented by those digits. As we increase the number 9 by 1 we start the one’s place position over at 0 again and the ten’s place (the one to the left of the ones place) is increased by 1. If no digit is already present to the left then the digit is considered a 0 so when it is increased by 1 it becomes a 1. As a number continues to increase, the 0 in the one’s place is increased until it reaches 9. At this point we have the value 19. If we increase it by 1 we start the one’s digit over again at 0 and increase the ten’s digit by 1 to get 2. This is the value 20. This system of incrementing the numbers continues into the hundreds, thousands, etc… places. In other words, this is just like an odometer for mileage in a car. Using this system to indicate the numbers 0 to 99 we express the 100 different combinations of the digits 0,1,2,3,4,5,6,7,8,9 that exists when the ones and tens places are used. The place positions are numbers 0, 1, 2, 3, etc… and correspond respectively to the place values one’s, ten’s, hundred’s, thousand’s, etc… This is also expressed by the powers of ten for each of the place position numbers. 10^0 = 1 (one’s place), 10^1=10 (ten’s place), 10^2=100 (hundred’s place), 10^3=1000 (thousand’s place), etc… A decimal (base 10) numbers value is derived by multiplying the digit (0 to 9) in each of the place position by 10 raised to the power of the place position number (0, 1, 2, 3, …). For example, the number 280 is 2*10^2 + 8*10^1 + 0*10^0 = 2*100 + 8*10 + 0 = 200 + 80 + 0 = 280.

Decimal Facts:

Base = 10

Digits in numbering system: 0,1,2,3,4,5,6,7,8,9

From this we see that we have numbering system that has a specific set of digits, digit place positions that correspond to the powers of the numbering system, and a systematic way of expressing all the combinations of digits for the number of places in the number. These same characteristics are used for other numbering systems that have a different base. For example, the binary numbering system is a base 2 system – based on the powers of 2 for each place position, the digits 0 and 1, and an analogous "odometer" system of expressing all the combinations of the digits 0 and 1 for the number of places in the number. The places in the binary system are the one’s, two’s, four’s, eight’s, sixteen’s, thirty-second’s, sixty-four’s, etc… place values.

Binary Facts:

Base = 2

Digits in numbering system: 0,1

Binary computers represent data by applying structured meaning to a series of ones and zeros. The structured meaning of these binary values represents data types such as logical, numeric and character. To apply a structured meaning to the data types, various size units and encoding methods are used.

In binary computers the mathematical property of the powers of two is a foundational concept. By definition, binary means two. In a binary computer each bit of information can be one of two binary values, either a one or a zero. This fact defines that all bits in the computer are either a one or a zero. When bits are grouped into various units, the number of different values (combination of ones and zeros) that unit can contain is determined by the number of bits in the group.

The table below shows various powers of two. The ^ symbol indicates that the base number, the number before the ^ is raised to the power of the number (exponent) after the ^. Raising a base number to the power of an exponent means to multiply the base number by the base number for the number of times indicated by the value of the exponent.

For example, 2^3 means to multiply 2 by the number 2, three times, 2 x 2 x 2 = 8.

0 to any power is 0.

2^0 = 1 (by definition any base number raised to the power of zero is one)
2^1 = 2 (any base number raised to the power of one is the base number)

Notice that there is a doubling of the values for each power, this is intuitive because multiplying anything by two doubles it.

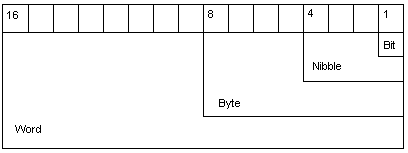
Bit – a bit is the smallest unit of storing data in a computer. It contains one binary digit either a one or a zero. There is only one place to put either a one or a zero in a bit so there is only two combination that exist. This is based on the principle of the powers of two; a bit has 2^1 = 2 combinations; either 0 or 1.

Nibble – a nibble, half a byte, is four bits grouped together. Each of these bits is a one or a zero. Since there are two distinct values each bit can contain and there are four bits in a nibble, sixteen possible combinations of ones and zeros exist that can be represented in a nibble. This is based on the principle of the powers of two; a nibble has 2^4 = 16 combinations. The table below shows the sixteen (16) different combinations of ones and zeros that can fit in a nibble.

1: 0000	5: 0100	9: 1000	13: 1100
2: 0001	6: 0101	10: 1001	14: 1101
3: 0010	7: 0110	11: 1010	15: 1110
4: 0011	8: 0111	12: 1011	16: 1111

The binary values represented in this table of 16 combinations are 0 to 15. This is elaborated on in the numeric data type and encoding section.

Byte – a byte is eight bits grouped together. Each of these bits is a one or a zero. Since there are two distinct values each bit can contain and there are eight bits in a byte, 256 possible combinations of ones and zeros exist that can be represented in a byte. This is based on the principle of the powers of two; a byte has 2^8 = 256 combinations. A byte has two nibbles, the left (most significant) nibble is referred to as the high nibble and the right (least significant) nibble is referred to as the low nibble.

Word – the definition of a word in a computer is dependent on the architecture of that particular computer’s Central Processing Unit (CPU). A word does not have a standard definition like bit, nibble and byte do. The most common definition of a word is a group of bits that are 16, 32 or 64 bits in length. The number of bits that define a word indicates the number of different values that can be represented in a word. The table in the principle of the powers of two section provides the number of combinations that 16, 32 and 64 bits represent.

Logical data types are used to represent a true or false value. This representation is called a Boolean value. By convention a zero (0) represents a value of false and a one (1) represents a value of true. This convention holds if the value is stored in one bit. If the value is stored in more than one bit then the convention is a zero (0) represents a value of false and any non-zero value represents a value of true.

Numeric data is stored in a computer as a series of ones and zeros. The number represented by the series is a binary number. However, because this series of ones and zeros can be long and hard for humans to read, other representations of the numeric values are used. These representations, in addition to binary, are octal, decimal or hexadecimal.

Binary – a binary number is a series of ones and zeros. This has been previously described in this document to a general extent. See the Principle of the Powers of Two and Size Units sections. Typically a binary number is read from right to left. The digit on the right is the least significant bit while the digit on the left is the most significant bit.

As the digits are read from right to left their significance goes from least to most. This means as a digit’s significance increases, its impact (significance) to the number is greater. For example given the decimal number 245, the 5 is in the ones position, the 4 is in the tens position and the 2 is in the hundreds position. The significance of changing the digit in the ones position is of the least significance in changing the relative value of the number. By changing the 5 to some digit between 0 and 9, then value of the whole number will change –5 to +4, or 240 to 249. On the other hand, changing the digit in the hundreds position has the most significance in changing the relative value of the number. By merely changing the 2 to a 3 the number becomes 345, that is a +100 change from 245. The same holds true for changing binary numbers.

In reading binary numbers from right to left, the right most bit is in bit position zero (0). The next bit to the left is in bit position one (1), and so on until the left most bit. In each bit position the digit can be either one or zero. The digit in bit position zero represents two to the power of one; meaning that the values that are in that number of positions (1) can be two different values (0 and 1). The digit in bit position one represents two to the power of two; meaning that the values that are in that number of positions (2) can have four different values (00, 01, 10, 11). These values represent the decimal numbers (0, 1, 2, 3) respectively. There are four combination but we start counting at zero so therefore the number ranges from zero to one less than the number of combinations (0 to 3). The reason that 00, 01, 10, 11 (binary) represents 0, 1, 2, 3 (decimal) respectively is based on the Principle of the Power of Two. The following table exemplifies the principle.

Binary #	Decimal #	Power of Two Calculation
00	0	0*(2^1) + 0*(2^0) = 0 + 0 = 0
01	1	0*(2^1) + 1*(2^0) = 0 + 1 = 1
10	2	1*(2^1) + 0*(2^0) = 2 + 0 = 2
11	3	1*(2^1) + 1*(2^0) = 2 + 1 = 3

Let’s dissect the power of two calculations. The binary # 01 is calculated by taking the digit in bit position zero, the 1 digit, and multiplying it by two to the power of zero, thus we have 1*(2^0) = 1*1 = 1. The digit is the next position, bit position one, a 0 digit is multiplied by two to the power of one, thus we have 0*(2^1) = 0*2=0. We then add them these two calculations together (1+0) to get 1.

Notice how this would progress with more digits extending to the left. Each digit is going to be either a 0 or 1 and it is multiplied by two to the power of the bit position number, (assuming that you start on the right, going left and counting from zero upwards by one). In other words, for bit position zero, 2^0 = 1 thus the binary digit is multiplied by one. For bit position one, 2^1 = 2 thus the binary digit is multiplied by two. For bit position two, 2^2 = 4 thus the binary digit is multiplied by four and so on.

Further notice that the range of numbers is one less than two raised to the number of binary digits there are. Given that a binary number has three digits, then the number of combinations of binary digits is 2^3 = 8 and the values are 0 to 7. (ie. The binary numbers 000, 001, 010, 011, 100, 101, 110, 111 equals 0, 1, 2, 3, 4, 5, 6, 7 in decimal respectively).

This further reveals the pattern of the powers of two. Take the binary number 101 which is the representation of the decimal number 5. It is calculated to be 5 by the formula 1*(2^2) + 0*(2^1) + 1*(2^0) = 1*4 + 0*2 + 1*1 = 5. 1*(2^2) is the binary digit 1 (on the left) multiplied by two to the power of two which is the bit position number. 0*(2^1) is the binary digit 0 (in the middle) multiplied by two to the power of one which is the bit position number. 1*(2^0) is the binary digit 1 (on the right) multiplied by two to the power of zero which is the bit position number.

The powers of two and the bit position work together. At bit position zero the power of two is zero (2^0) which equals one. At bit position one the power of two is one (2^1) which equals two, at bit position two the power of two is two (2^2) which equals four, at bit position three the power of two is three (2^3) which equals eight, etc…

2^0=1, 2^1=2, 2^2=4, 2^3=8, 2^4=16. Notice that we start with one and double it to get the next number (2), then double it to get 4, then 8, then 16, etc… See how this relates to the powers of two table.

As a final example let’s examine the following diagram.

Binary #	1	0	0	1	1	0	1	1
Bit Position	7	6	5	4	3	2	1	0

Calculation of the binary representation of the decimal number:

Binary Digit	Bit Position	Calculation
1	7	1*(2^7) = 128
0	6	0*(2^6) = 0
0	5	0*(2^5) = 0
1	4	1*(2^4) = 16
1	3	1*(2^3) = 8
0	2	0*(2^2) = 0
1	1	1*(2^1) = 2
1	0	1*(2^0) = 1

128+0+0+16+8+0+2+1 = 155 (decimal)

So for a byte which has eight binary digits in bit position zero to seven you take the binary digit value (0 or 1) and multiply it by two to the power of the bit position number and then add all the results together.

Binary Digit	Bit Position	Calculation
A	7	S = A*(2^7) = A*128
B	6	T = B*(2^6) = B*64
C	5	U = C*(2^5) = C*32
D	4	V = D*(2^4) = D*16
E	3	W = E*(2^3) = E*8
F	2	X = F*(2^2) = F*4
G	1	Y = G*(2^1) = G*2
H	0	Z = H*(2^0) = H*1

S + T + U + V + W + X + Y + Z = decimal number

Octal – This is another numbering scheme used in computers that is easier to work with than a long series of binary digits. In similar fashion to binary numbers which have only two digits (0 & 1) and is known as a base 2 numbering system, octal has eight digits (0 to 7) and is known as a base 8 numbering system. This means that as you count in octal, you start at zero and go to seven. When you add one more to seven then the octal number has two digits. The left digit will become a one (1) and the right digit a zero (0); ie 10. Humans are used to decimal numbers that are base 10, so when we see 10 we think it is a ten. In octal notation though, %o10 is the equivalent of 8 in decimal. It is like an odometer, when the right side digit goes past seven a digit is incremented on the left by one and the seven restarts back at zero. Thus when, %o10 (octal) is incremented seven more times the octal number is %o17 (octal). Then if it is incremented again the digit on the left is incremented by one more, thus it becomes a 2 and the seven is restarted at 0 – then octal number is now %o20 (octal) which is 16 in decimal. In other words the numbering system counts in units of eight hence the name octal. Since it takes three bits to encode the octal number range 0 to 7, octal is most often used when working with groupings of three bits; which is not very often.

Decimal – This is the base 10 numbering system that humans are most used to. It has ten distinct digits (0 to 9). As you count up to nine and then add one more you increment the digit to the left by one and restart the nine at zero; ie 9 incremented by 1 is 10. Since computers are based on the binary numbering system it does not directly work with decimal numbers. The decimal numbers are encoded into their binary equivalents and operated upon. The octal and hexadecimal numbering system are not directly used by computers either but since they are a power of two (8 and 16) then they are more easily converted from binary. That is why octal and more often hexadecimal numbering is used in computers.

Hexadecimal – This is a base 16 numbering system. It offers a convenient method to represent binary numbers in a shorter notation. The hexadecimal numbering system has sixteen distinct digits (0 to 9 and A to F), where 0 to 9 is the same as in decimal and A=10, B=11, C=12, D=13, E=14, F=15. Similar to other numbering systems hexadecimal counts from 0 to F and then when incremented by one more a digit is incremented on the left by one and the F is restarted at zero; ie 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, and then 10. The F has "wrapped-around" to 0 and the digit to the left (an implied 0) is incremented by 1. Now the number takes two digits to describe its value. To indicate that a number represents a hexadecimal number it is usually written in sets of two digits at a time and preceded by a $ character. Thus we write the decimal numbers 0 to 16 in hexadecimal as $00, $01, $02, $03, $04, $05, $06, $07, $08, $09, $0A, $0B, $0C, $0D, $0E, $0F, $10. Each place in a hexadecimal number can represent the binary number in a nibble (four bits). Remember that a nibble has sixteen combinations ranging from 0 to 15 (0000 to 1111 in binary). In hexadecimal this corresponds to $00 to $0F. Two hexadecimal digits can represent all the possible values in a byte (8 bits), 0 to 255 (256 combinations); this would be $00 to $FF. This is a much more convenient notation to use than the binary numbers 00000000 to 11111111. With each hexadecimal pair the left digit represents the high nibble and the right digit represents the low nibble.

In the Binary Number Calculation section it is explained and demonstrated how to convert a binary number into its decimal equivalent. Converting numbers from binary to octal and hexadecimal and visa versa is done most easily by equating bit patterns with octal or hexadecimal values and visa versa. For example, by using the tables below we can convert "00 100 101" binary to its octal equivalent. Notice that the binary digits are in groups of three starting from the right and going left. The left most set of binary digit is the remaining group of digits that is three or less. The missing digits in this last group are assumed to be 0. The "00" on the left is octal digit 0, the "100" in the middle is octal digit 4, and the "101" on the right is octal digit 5. Thus this binary number is equivalent to %o045 (octal). The method of conversion is to break the binary digits into groups of three with the left most group being a group of three or less and then equating each group with its octal equivalent based on the table below. Over time this conversion should be able to be done from memory.

Binary and Octal Equivalency Table:

To convert binary digits to their hexadecimal equivalents is very similar. The difference is that the binary digits are broken up into groups of four digits, still right to left with the remaining digits on the left most group being four or less digits with the missing digits being zeros. Each group of four digits is looked up in the table to find its hexadecimal counterpart. Again, over time this conversion can be done from memory. For example, "10001010" in binary is broken up into two groups; "1000" and "1010". These groups are equal to the hexadecimal digits 8 and A respectively, making $8A. Converting from hexadecimal to binary is shown in another example. $F7 is "1111" and "0111" respectively, making "11110111".

Binary and Hexadecimal Equivalency Table:

Now that numbers can be converted from binary to decimal, octal and hexadecimal, we turn our attention to converting from decimal, octal and hexadecimal to binary. To convert from decimal to binary involves dividing the decimal number by two and taking the remainder, which will be either 0 or 1 to be the binary digit. The quotient, which is the value the decimal number can be divided by two is, is then divided by two until the quotient is zero. These successive divisions will produce a series of binary digits starting with the least significant bit to the most significant bit.

For example, to convert the decimal number eleven (11) to binary the following calculations are done:

The binary equivalent is "1011" (read right-most column above from bottom to top (MSB to LSB)).

Similar conversion could be done from decimal to hexadecimal by dividing by 16, and to octal by dividing by 8.

For example, 256 (decimal) is done with:

This becomes $0100 which is 256.

Conversion Table:

The addition rules for binary numbers are straightforward. The rules are:

where (1) denotes a "carry" of 1 to the left. Note that 1 + 1 = 2 and the binary "10" is decimal 2.

Other examples are:

* Notice that carrying occurred twice.

So far we have only dealt with positive integer numbers. We need to introduce a scheme to represent negative integers. In signed binary representation, the left-most bit is used to indicate the sign of the number. Traditionally, "0" is used to denote a positive number and "1" is used to denote a negative number. This "11111111" will represent –127 and "01111111" denotes +127. With the introduction of the sign bit the range of numbers changes. The range is now –127 to 127 instead of 0 to 255. Now let’s revisit binary addition using signed numbers.

Take for example the addition o f"-5" to "+7".

This is not the correct result. The correct result should be +2. Since we must operate on binary data as well as represent it we use a different scheme than signed binary. This scheme is called two’s complement representation.

To understand two’s complement representation and how it produces correct arithmetic results let’s first learn what one’s complement is. Positive numbers are represented in their normal binary format. For example, "+3" is represented as usual by 00000011. However, its complement "-3" is obtained by complementing each bit. Each 0 is changed to a 1 and each 1 is changed to a 0 thus we have 11111100 being the one’s complement representation of "-3". Even with one’s complement addition does not always yield the correct result.

Examine the following examples.

The correct result should be "00000010" or "2".

The correct result should be "11111010" or "-5".

Therefore we must have something better than one’s complement.

Two’s complement is the solution to representing signed binary integer that also yields correct arithmetic results. Positive numbers are still represented as normal. The difference lies in the representation of negative numbers. This is because the representation of negative numbers in the source of the incorrect arithmetic in the signed binary and one’s complement representations. To obtain the two’s complement of a number we first compute the one’s complement and then add one.

Let’s examine the examples of 3 + 5 and 3 – 5.

The one’s complement of 11111110 is 00000001, then add 1 and we get 00000010 which is "+2", therefore, 11111110 correctly represents "–2". (ie. 11111101 + 1 = 11111110).

With two’s complement representation the range of signed binary values that can be recorded in eight (8) bits is –128 to 127. The reason for this is that in seven (7) bits 128 different combinations can be recorded. For negative numbers the range is –1 to –128. For positive numbers the range is 0 to 127; notice that in this sense zero (0) is considered a positive number. As the number of bits increases so does the range of numbers increase.

The bit patterns for the numbers from 0 to 127 follow the scheme based on the powers of two such that 0 is 00000000 and 127 is 11111111. For the negative numbers –1 to –128 in two’s complement representation the bit pattern is such that if the two’s complement bit string bits are reversed and 1 is added (the reverse operation of two’s complement) then the bit pattern will look just like the corresponding positive number.

For example, -128 is 1000000, the high bit signifies the number is negative and the remaining seven bits are all 0’s. If we reverse the bits we get 01111111 and then do a binary add of 1 we get 10000000, this is the bit pattern for +128. Again, -1 is 11111111, the high bit signifies the number is negative and the remaining seven bits are all 1’s. If we reverse the bits we get 00000000 and then do a binary add of 1 we get 00000001, this is the bit pattern for +1.

The conclusion of binary addition and two’s complement is that the computer can only do addition, so for negative numbers and subtraction, two’s complement must be used. Therefore, if you are adding numbers together and they are in two’s complement format, you simply to a binary addition according to the rules described above. There is no need to do any conversion of the binary numbers. If you are doing a subtraction operations then the second number needs to be converted to it’s two’s complement format, whether it is a positive or negative number and then a binary addition is done. The result will be the correct answer in two’s complement format. Since the computer can only do addition and cannot do subtraction, when you want to subtract you take the complement of the second operand and add (ie. 12 – 3 is the same as 12 + (-3), or 12 – (-20) is the same as 12 + 20).

Otherwise known as BCD, this numbering scheme is used to obtain complete precision while working with decimal numbers. Base 10 numbers with a decimal point and a sign (+ or -) is encoded in binary in this scheme. The cost of the complete precision is more memory is required to represent the decimal number and slow arithmetic operations. The basic idea is to encode each decimal digit (0 to 9) into its binary equivalent. The binary codes for each decimal digit is stored in a nibble. As we already know a nibble can contain sixteen binary digit combinations but with BCD only ten of them are used, thus the first waste of memory is introduced. The sign of the number either positive (+) or negative (-) is store in a nibble as 0000 and 0001 respectively. This also waste three bits because we could distinguish between + or – with only one bit. Additional nibbles or bytes are used to indicate the number of digits in the BCD number and the number of digits to the left that the decimal point is located. If a nibble is used for each of these items then the BCD number could have fifteen digits at most.

For example, +2.41 may be represented by:

1. 3 digits
2. the "." is on the left of digit 4 (2 digits over).
3. It is a positive number.

As we have learned, computers work with binary numbers. These numbers are inherently integers and not even decimal based integers at that. This makes arithmetic difficult in computers, particularly when interfacing with human who use the decimal numbering system and often used numbers that are not integers; ie floating point numbers like 163.72. Therefore, the computer has to represent floating point decimal numbers using only binary digits to do so. Several schemes have been developed to do this. The goal of the schemes is to maintain accurate and precise representation of floating point decimal numbers and to particularly yield accurate and precise results when arithmetic is done upon the floating point numbers. The Java standard for floating point numbers is IEEE 754 floating point. See http://www.psc.edu/general/software/packages/ieee/ieee.html

[Exercise: Programming Basics Data Representation Size and Numeric]

Again since computers only work with binary digits, characters (the alphabet, symbols that can be typed on a keyboard, and other control codes) must be represented in a series of binary digits. For this reason several methods of encoding characters into binary numbers have been developed. ASCII and EBCDIC have emerged as the standards but they are limited in the number of different characters they can represent. Since computers have pervaded nearly all societies, the need to be able to encode more characters, particularly non-English languages, has necessitated the need for a new standard; Unicode is an attempt at establishing this new standard.

ASCII – The ASCII (American Standard Code for Information Interchange) character coding scheme uses one byte for each character. The most basic form of the ASCII system is called ASCII-7. ASCII-7 uses only seven of the eight bits in a byte to encode characters. The most significant character (the left most one) is always zero. Therefore, only 128 different characters can be encoded with ASCII-7. This is enough for the English alphabet and punctuation, some other symbols and some non-printable control characters. These characters are uniquely assigned a binary value between 0 and 127. In a sense the assignments are arbitrary but the assignments do follow a logical scheme so that the sorting of characters produces understandable results. See the following table. To get more characters ASCII also has a standard that uses 8 bits. This allows for 256 different characters. The first 128 are the same as ASCII-7 and the next 128 characters are defined by the ISO Latin-1 standard, which incorporates most Western language characters.

The following is the ASCII-7 Table of characters and their hexadecimal equivalents. The multi-character items are non-printable control characters. These are defined in the next table. You can calculate the numeric value of a character by constructing a 2-digit hexadecimal number in which the column position of the character represents the high nibble of the hexadecimal number and the row position of the character represents the low nibble of the number. For example, an uppercase A has a numeric value of $41 (hexadecimal).

Note: digit zero (0) starts at $30 (48 decimal) and proceeds to $39 which is nine (9).
Note: ‘A’ starts at $41 (65 decimal) and lowercase ‘a’ starts at $61 (97 decimal) and both proceed in-sync to Z ($5A, 90 decimal) and z ($7A, 122 decimal) respectively.

These are good things to remember because it can help you to quickly recognize the codes for these characters.

Other common and useful codes to remember are:

ASCII-7 Control character definitions table:

More detailed information can be found in the Digital VT420 Programmer Reference Manual, though this has lots of device specific information and is beyond the scope of what most programmers need to know about ASCII nowadays.

EBCDIC – The EBCDIC (Extended Binary Coded Decimal Interchange Code) coding scheme is the IBM standard. Except in the IBM world it is mostly out of favor. The same basic idea as ASCII is present but different values are placed with each character. There is still a system of logic to the assignments so that sorting can be properly done. There are also more and different control characters. This standard uses all eight bits of a byte to encode characters thus there are 256 possible characters.

Unicode – This is a 16-bit (two byte) character encoding scheme. The 65,536 combinations of 16 bits allows for virtually every written language in common use on the planet to be encoded. There are provisions that make Unicode backward compatible with ASCII-7 and ISO Latin-1. Unicode does double the amount of space to store a character. When a character can be encoded with only one byte the high byte is all zeros.

[Exercise: Programming Basics Data Representation Character Coding]

Note that the computer has no way of knowing if a series of binary digits represents an integer or floating point number, a logical value or a character. Some other external mechanism is used to apply a semantic meaning to the series of binary digits. Defining the binary digits in memory to be of a particular type typically does this. Computer memory is allocated for each distinct element of data. The type they are defined as determines the amount of memory and what the binary digits represent. This leads into the next section about basic programming and the use of variables. A program and the constructs it uses help to supply the external meaning to apply to the binary digits in the computer’s memory.

[Index] [Next]